05 Nov 2008 -
--==[ Persamaan Logaritma ]==--
Persamaan logaritma adalah persamaan yang peubahnya terdapat dalam bilangan pokok atau numerusnya.
Bentuk persamaan logaritma pada umumnya belum sederhana. Untuk menyederhanakan persamaan logaritma perlu memperhatikan sifat-sifat logaritma berikut :
1. numerus pada persamaan semula bernilai positif.
2. bilangan pokok logaritma pada persamaan semula bernilai positif dan tidak
sama dengan 1 (satu).
Contoh soal dan penyelesaian.:
--==[Fungsi Logaritma]==--
Fungsi Logaritma adalah suatu fungsi invers (balikan) dari fungsi eksponen. Bila fungsi eksponen dinyatakan dengan f(x) = ax, a > 0, a ≠ 1, maka invers dari f(x0 ditulis dengan f-1(x) = a log x atau f(x) = a log x, a > 0, a ≠ 1.
Secara umum bila y = ax, maka x = a log y.
*) Bila f(x) = a log x, dengan a > 1, x > 0 , x E R, maka f(x) dikatakan fungsi turun.
*) Bila f(x) = a log x, dengan 0 < a < 1, x > 0 , x E R, maka f(x) dikatakan fungsi naik.
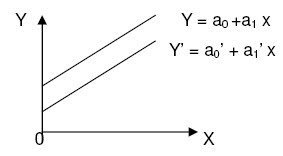
Grafik fungsi logaritma selalu melalui titik (1,0) dan selalu berada di sebelah
kanan sumbu Y. Perhatikan gambar di bawah ini.
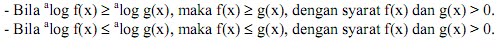
Contoh soal :

Kesimpulan ; Himpunan penyelesaiannya adalah { x < -1 atau x > 2}
»» READMORE...
Persamaan logaritma adalah persamaan yang peubahnya terdapat dalam bilangan pokok atau numerusnya.
Dalam menyelesaikan persamaan logaritma, bilangan pokok logaritma perlu disamakan dahulu. Nilai penyelesaian yang diperoleh perlu diuji dengan mensubstitusikan ke persamaan semula. Nilai penyelesaian yang menjadi anggota himpunan penyelesaian (HP) adalah yang mengakibatkan :
1. numerus pada persamaan semula bernilai positif.
2. bilangan pokok logaritma pada persamaan semula bernilai positif dan tidak
sama dengan 1 (satu).
Contoh soal dan penyelesaian.:
Fungsi Logaritma adalah suatu fungsi invers (balikan) dari fungsi eksponen. Bila fungsi eksponen dinyatakan dengan f(x) = ax, a > 0, a ≠ 1, maka invers dari f(x0 ditulis dengan f-1(x) = a log x atau f(x) = a log x, a > 0, a ≠ 1.
Secara umum bila y = ax, maka x = a log y.
*) Bila f(x) = a log x, dengan a > 1, x > 0 , x E R, maka f(x) dikatakan fungsi turun.
*) Bila f(x) = a log x, dengan 0 < a < 1, x > 0 , x E R, maka f(x) dikatakan fungsi naik.
Grafik fungsi logaritma selalu melalui titik (1,0) dan selalu berada di sebelah
kanan sumbu Y. Perhatikan gambar di bawah ini.
--==[Pertidaksamaan logaritma]==--
Dari grafik fungsi logaritma di atas tampak bahwa :
1. Untuk a > 1 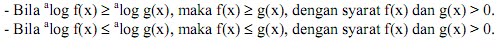
Contoh soal :
Kesimpulan : Nilai x yang menjadi penyelesaian pertidaksamaan harus memenuhi (1) dan (2) Jadi nilai x yang memenuhi adalah x > 4
2. Untuk 0 < a < 1

Kesimpulan ; Himpunan penyelesaiannya adalah { x < -1 atau x > 2}